Abb. 1
| 4 | = | 2 + 2 | |
| 6 | = | 3 + 3 | |
| 8 | = | 3 + 5 | |
| 10 | = | 3 + 7 = | 5 + 5 |
| ... |
|
|
|
|
|
|
|
|
|
|

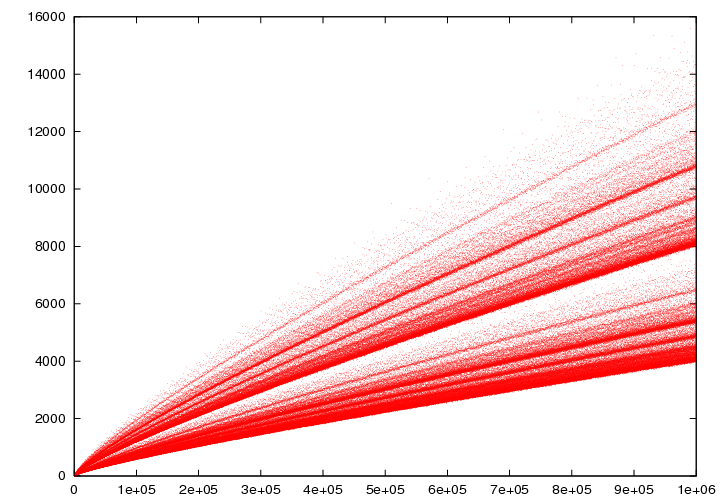
 Hier sind die Punktfarben nach σ0(z) gewählt (oberer Farbbalken). Außerdem sind drei Kurven
f(z) = c f0(z) = c 2z/ln²(z) für c = [0.7, 1.5, 3.0] eingezeichnet.
Hier sind die Punktfarben nach σ0(z) gewählt (oberer Farbbalken). Außerdem sind drei Kurven
f(z) = c f0(z) = c 2z/ln²(z) für c = [0.7, 1.5, 3.0] eingezeichnet. Rot (σ0(z)=2) sind alle Primzahlen z = p
(diese haben natürlich immer ua. die triviale
Zerlegung 2p = p + p). Orange (σ0(z)=4) sind alle Zahlen der Form
Rot (σ0(z)=2) sind alle Primzahlen z = p
(diese haben natürlich immer ua. die triviale
Zerlegung 2p = p + p). Orange (σ0(z)=4) sind alle Zahlen der Form

Ein Gnuplot aller Zerlegungen der ersten 1,000,000 PZ ergibt zB. einen optimalen Fit
(der Koeffizient im Logarithmus wurde ausprobiert) mit
ngz(p) ≈ f(p) = 1.3115⋅p/ln²(0.666⋅p)
mit einer Standard-Abweichung von δ = 112.7 und einer
max. Abweichung δmax=648.1 (für p=14,395,261, ngz(p)=72,406).
Erstaunlich ist die sehr geringe Streuung der Punkte (im Vergleich zu oben). Die max. rel. Abweichung ist kleiner als 1% und wird
für größere p immer kleiner.
 Eine Histogramm-Darstellung der Verteilung der Goldbach-Zahlen über f = c f0(n) = cn/ln²(0.666⋅n)
zeigt klare Maxima für den Quotienten c = 1.3116, 2.6232 und ein breites Minimum bei c ≈ 2.45.
Die beiden Maxima fallen mit denen von σ0(z) = 2,4 zusammen.
Eine Histogramm-Darstellung der Verteilung der Goldbach-Zahlen über f = c f0(n) = cn/ln²(0.666⋅n)
zeigt klare Maxima für den Quotienten c = 1.3116, 2.6232 und ein breites Minimum bei c ≈ 2.45.
Die beiden Maxima fallen mit denen von σ0(z) = 2,4 zusammen.
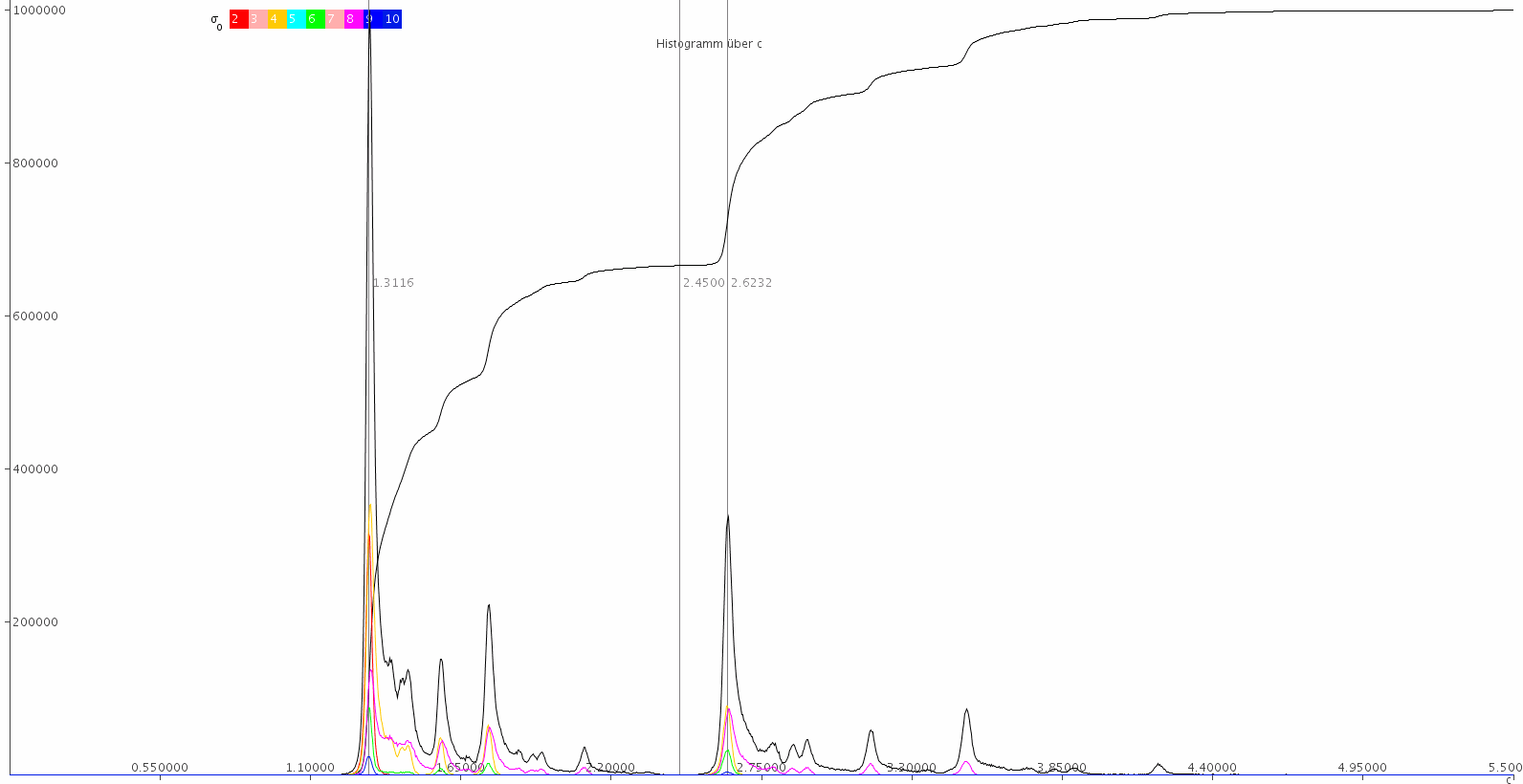 Auch hier sind die Histogramme der Teilmengen σ0(z) = 2,4,6,8,10 dargestellt,
wobei für 2 eine eingipflige VF zu erkennen ist (mit Max bei 1.3116).
Die absoluten Minima und Maxima der Werte von c(z) sind cmin = 0.160 (für z = 3) und
cmax = 5.426 (für z = 510510 = 2⋅3⋅5⋅7⋅11⋅13⋅17).
Auch hier sind die Histogramme der Teilmengen σ0(z) = 2,4,6,8,10 dargestellt,
wobei für 2 eine eingipflige VF zu erkennen ist (mit Max bei 1.3116).
Die absoluten Minima und Maxima der Werte von c(z) sind cmin = 0.160 (für z = 3) und
cmax = 5.426 (für z = 510510 = 2⋅3⋅5⋅7⋅11⋅13⋅17).
Tab. 2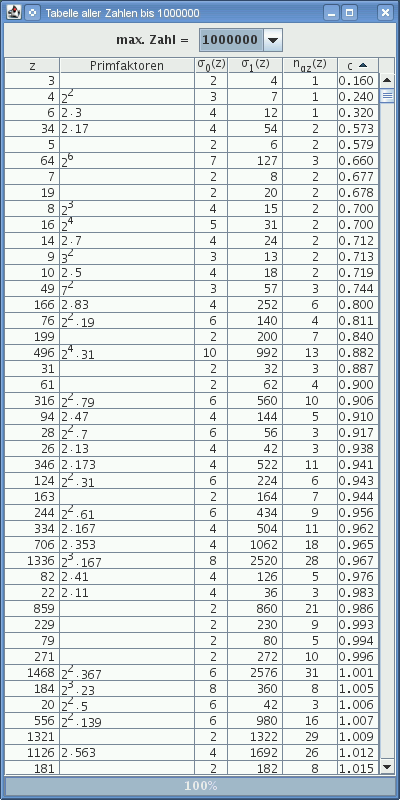
| Tab. 3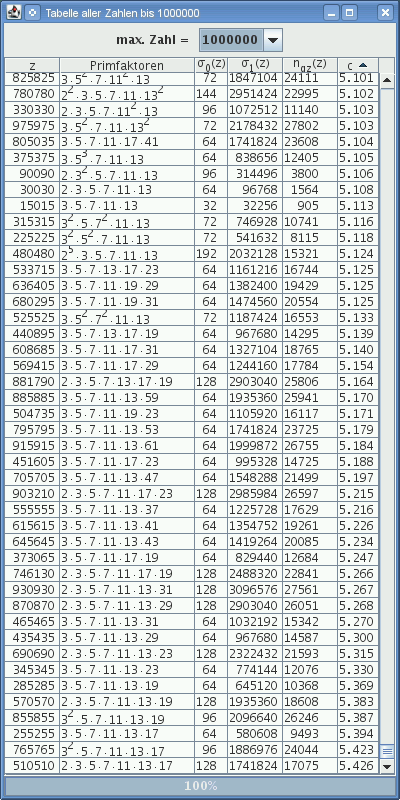
|
| f | z | c | δ |
|---|---|---|---|
| 1,2,4,8 | 2n p, n ≥ 0 | 1.3112 | 82.5 |
| 3,6,9 | 2n 3m p, n ≥ 0, m > 0 | 2.6223 | 109.5 |
| 5,10 | 2n 5m p, n ≥ 0, m > 0 | 1.7482 | 92.4 |
| 7 | 2n 7m p, n ≥ 0, m > 0 | 1.5734 | 88.3 |
| p | ngz(p) | ngz(2p) | ngz(3p) | ngz(4p) | ngz(5p) | ngz(6p) | ngz(7p) | ngz(8p) | ngz(9p) | ngz(10p) |
|---|---|---|---|---|---|---|---|---|---|---|
| ... | ||||||||||
| 100003 | 1071 | 1869 | 5306 | 3372 | 5421 | 9555 | 6405 | 6014 | 13493 | 9688 |
| 100019 | 1045 | 1878 | 5279 | 3386 | 5485 | 9467 | 6495 | 5967 | 13306 | 9757 |
| 100043 | 1060 | 1867 | 5256 | 3357 | 5456 | 9530 | 6527 | 6013 | 13366 | 9684 |
| 100049 | 1072 | 1896 | 5284 | 3357 | 5393 | 9540 | 6487 | 6007 | 13334 | 9801 |
| ... | ||||||||||
| 200003 | 1907 | 3323 | 9561 | 6024 | 9601 | 17108 | 11641 | 10848 | 23976 | 17583 |
| 200009 | 1897 | 3343 | 9387 | 6122 | 9757 | 16910 | 11591 | 10910 | 24034 | 17607 |
| 200017 | 1872 | 3348 | 9474 | 5969 | 9781 | 17144 | 11603 | 10940 | 24104 | 17575 |
| ... | ||||||||||
| 300007 | 2595 | 4750 | 13309 | 8536 | 13730 | 24185 | 16486 | 15348 | 34275 | 24900 |
| 300017 | 2682 | 4729 | 13221 | 8484 | 13728 | 24051 | 16414 | 15408 | 34184 | 24963 |
| 300023 | 2612 | 4693 | 13341 | 8490 | 13674 | 24088 | 16545 | 15439 | 34282 | 24888 |
| ... | ||||||||||
| 400009 | 3325 | 5980 | 17058 | 10906 | 17522 | 31104 | 21117 | 19666 | 43522 | 31953 |
| 400031 | 3358 | 6004 | 17063 | 10913 | 17518 | 30671 | 21096 | 19805 | 43706 | 32032 |
| 400033 | 3384 | 6030 | 17064 | 10938 | 17461 | 30847 | 21114 | 19796 | 43822 | 31899 |
| ... | ||||||||||
| f | samples | pmax | c(f) | c(f)/c(1) | δ | dmax |
|---|---|---|---|---|---|---|
| 1 | 2085615 | 33933979 | 1.3138 | 1.000 | 160.5 | 1014.4 |
| 2 | 1089318 | 16966991 | 1.3138 | 1.000 | 160.2 | 1039.7 |
| 3 | 745696 | 11311319 | 2.6276 | 2.000 | 213.5 | 1464.4 |
| 4 | 570075 | 8483479 | 1.3138 | 1.000 | 160.0 | 950.3 |
| 5 | 463046 | 6786761 | 1.7517 | 1.333 | 179.4 | 1088.8 |
| 6 | 390754 | 5655659 | 2.6276 | 2.000 | 213.4 | 1232.7 |
| 7 | 338543 | 4847699 | 1.5766 | 1.200 | 171.5 | 973.8 |
| 8 | 299043 | 4241723 | 1.3138 | 1.000 | 160.0 | 964.5 |
| 9 | 268043 | 3770381 | 2.6276 | 2.000 | 213.0 | 1168.0 |
| 10 | 243094 | 3393373 | 1.7517 | 1.333 | 179.1 | 961.2 |
| 11 | 222479 | 3084901 | 1.4598 | 1.111 | 165.5 | 1085.1 |
| 12 | 205267 | 2827823 | 2.6276 | 2.000 | 212.9 | 1254.7 |
| 13 | 190552 | 2610287 | 1.4332 | 1.091 | 164.8 | 1058.4 |
| 14 | 177918 | 2423851 | 1.5766 | 1.200 | 171.1 | 1053.9 |
| 15 | 166927 | 2262233 | 3.5035 | 2.667 | 236.8 | 1300.5 |
| 16 | 157246 | 2120863 | 1.3138 | 1.000 | 159.5 | 909.2 |
| 17 | 148650 | 1996109 | 1.4014 | 1.067 | 162.5 | 977.9 |
| 18 | 141001 | 1885207 | 2.6276 | 2.000 | 213.7 | 1279.2 |
| 19 | 134091 | 1785977 | 1.3911 | 1.059 | 162.1 | 911.8 |
| 20 | 127902 | 1696697 | 1.7517 | 1.333 | 179.2 | 983.8 |
| 21 | 122253 | 1615891 | 3.1531 | 2.400 | 226.9 | 1342.5 |
| 22 | 117137 | 1542451 | 1.4598 | 1.111 | 164.9 | 939.5 |
| 23 | 112415 | 1475387 | 1.3764 | 1.048 | 162.0 | 1033.8 |
| 24 | 108092 | 1413889 | 2.6276 | 2.000 | 213.4 | 1236.6 |
| 25 | 104074 | 1357351 | 1.7517 | 1.333 | 179.2 | 1048.3 |
 Den direkten Vergleich der GZ (rot) mit den NGZ (grün) zeigt die folgende Abb. bis z = 1,000,000 :
Den direkten Vergleich der GZ (rot) mit den NGZ (grün) zeigt die folgende Abb. bis z = 1,000,000 :
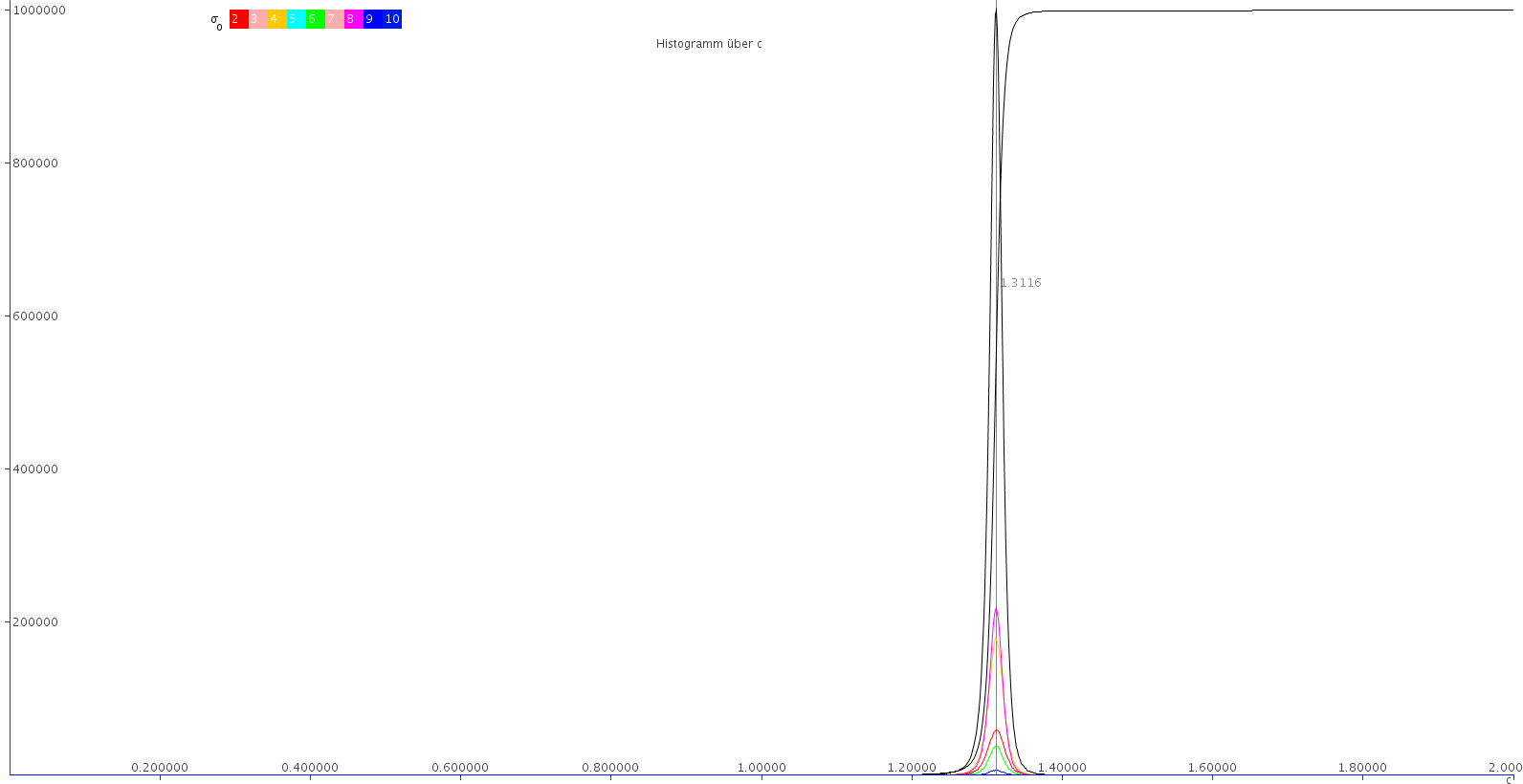
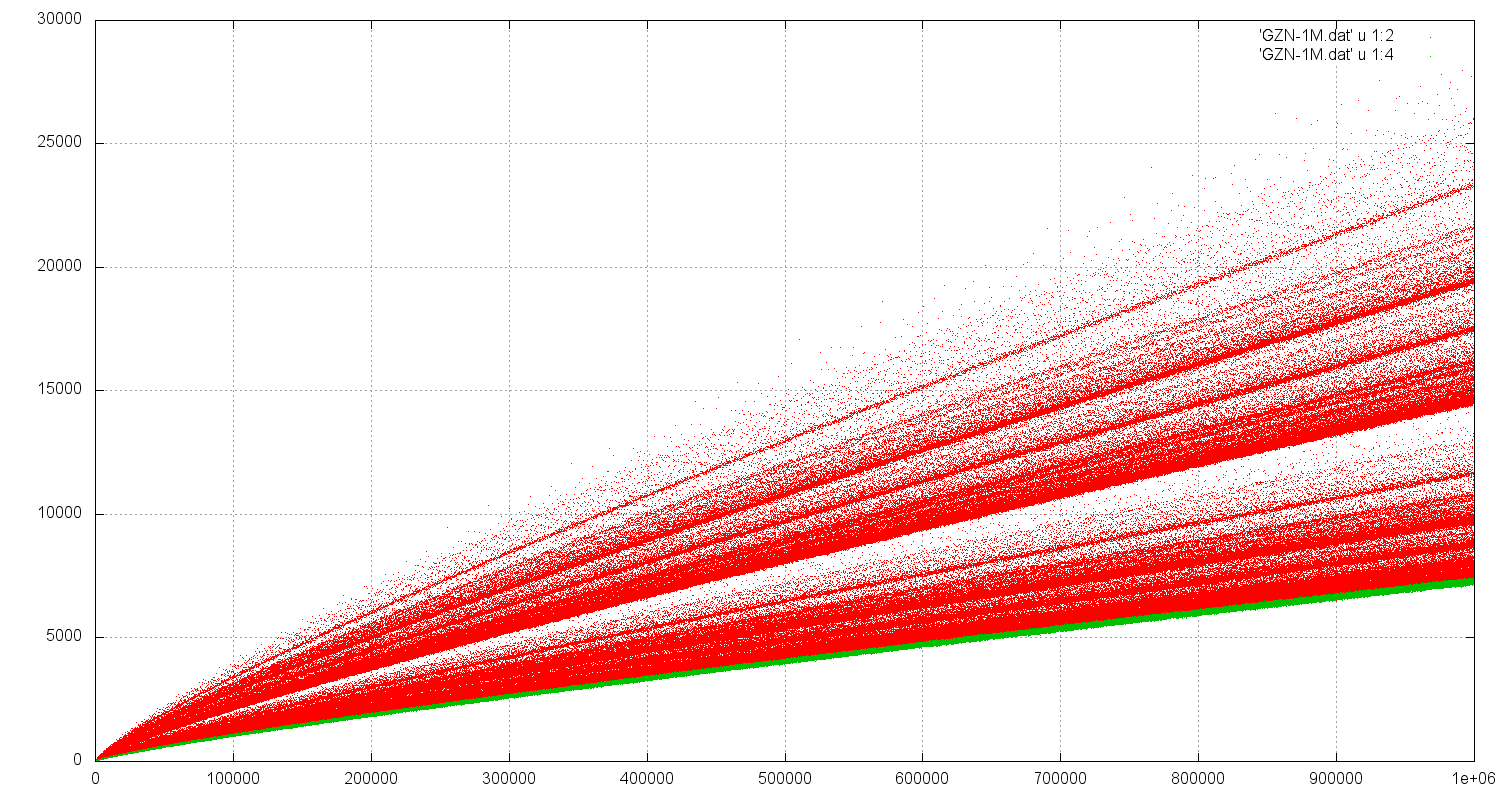 Das entsprechende Histogramm der normierten GZ zeigt klassische Gaußverteilungen
(hier ist die c*-Skala im Vergleich zu Abb. 6 verkürzt), mit einem
Minimum von c*min = 0.08 (für z=3) und Maximum von c*max = 1.652 (für z=71), die auch unabhängig
von σ0 zu sein scheinen (visuell).
Das entsprechende Histogramm der normierten GZ zeigt klassische Gaußverteilungen
(hier ist die c*-Skala im Vergleich zu Abb. 6 verkürzt), mit einem
Minimum von c*min = 0.08 (für z=3) und Maximum von c*max = 1.652 (für z=71), die auch unabhängig
von σ0 zu sein scheinen (visuell).
 Ein Ausschnitt einer Tabelle, bei der diese Normierung angewandt wird,
ergibt zB (die Spalten mit dem '*' kennzeichnen die entsprechenden
normierten Werte):
Ein Ausschnitt einer Tabelle, bei der diese Normierung angewandt wird,
ergibt zB (die Spalten mit dem '*' kennzeichnen die entsprechenden
normierten Werte):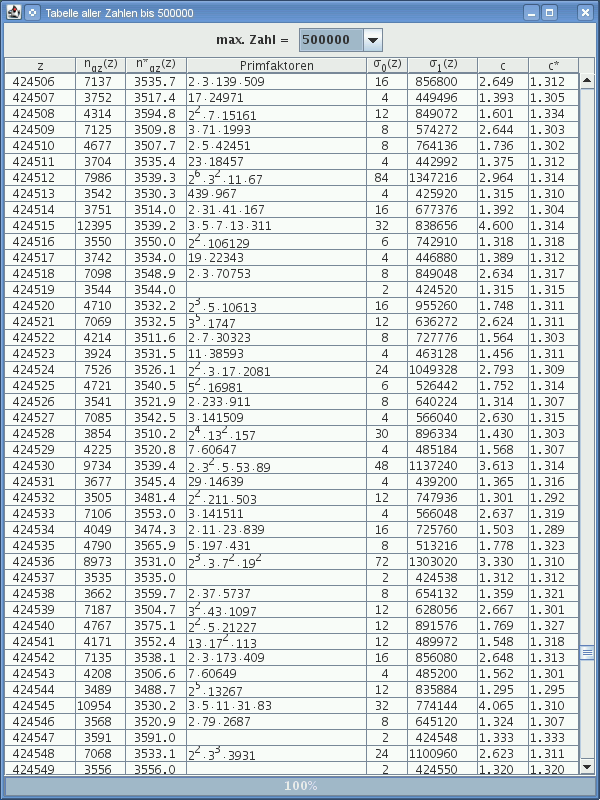
| z-Intervall | c*min | (bei z) | c*max | (bei z) |
|---|---|---|---|---|
| 3 - 49999 | 0.0798 | 3 | 1.6516 | 71 |
| 50000 - 99999 | 1.2086 | 72064 | 1.3981 | 53993 |
| 100000 - 149999 | 1.2393 | 142684 | 1.3868 | 103567 |
| 150000 - 199999 | 1.2499 | 172751 | 1.3747 | 185141 |
| 200000 - 249999 | 1.2497 | 239566 | 1.3666 | 200726 |
| 250000 - 299999 | 1.2532 | 265411 | 1.3648 | 269261 |
| 300000 - 349999 | 1.2590 | 303904 | 1.3594 | 302936 |
| 350000 - 399999 | 1.2606 | 361486 | 1.3626 | 356216 |
| 400000 - 449999 | 1.2669 | 409246 | 1.3584 | 433781 |
| 450000 - 499999 | 1.2664 | 477329 | 1.3562 | 469757 |
| 500000 - 549999 | 1.2673 | 522326 | 1.3510 | 524350 |
| 550000 - 599999 | 1.2703 | 562924 | 1.3521 | 558091 |
| 600000 - 649999 | 1.2701 | 612022 | 1.3522 | 630068 |
| 650000 - 699999 | 1.2682 | 685291 | 1.3499 | 677762 |
| 700000 - 749999 | 1.2754 | 718456 | 1.3509 | 704294 |
| 750000 - 799999 | 1.2719 | 791299 | 1.3453 | 786152 |
| 800000 - 849999 | 1.2760 | 841546 | 1.3492 | 847472 |
| 850000 - 899999 | 1.2764 | 899629 | 1.3441 | 859589 |
| 900000 - 949999 | 1.2772 | 915253 | 1.3415 | 914477 |
| 950000 - 999999 | 1.2772 | 954094 | 1.3448 | 972347 |
| k | c* | δ | dmax | bei z |
|---|---|---|---|---|
| 0.600 | 1.2899 | 28.463 | 187.7 | 972347 |
| 0.605 | 1.2915 | 28.445 | 187.4 | 972347 |
| 0.610 | 1.2932 | 28.427 | 187.2 | 972347 |
| 0.615 | 1.2948 | 28.411 | 187.0 | 972347 |
| 0.620 | 1.2964 | 28.396 | 186.7 | 972347 |
| 0.625 | 1.2980 | 28.382 | 186.5 | 972347 |
| 0.630 | 1.2996 | 28.370 | 186.3 | 972347 |
| 0.635 | 1.3012 | 28.358 | 186.0 | 972347 |
| 0.640 | 1.3028 | 28.348 | 185.9 | 847472 |
| 0.645 | 1.3044 | 28.338 | 185.8 | 847472 |
| 0.650 | 1.3059 | 28.330 | 185.6 | 847472 |
| 0.655 | 1.3075 | 28.322 | 185.5 | 847472 |
| 0.660 | 1.3090 | 28.316 | 185.4 | 847472 |
| 0.665 | 1.3105 | 28.310 | 185.3 | 847472 |
| 0.670 | 1.3120 | 28.306 | 185.1 | 847472 |
| 0.675 | 1.3135 | 28.302 | 185.0 | 847472 |
| 0.680 | 1.3150 | 28.299 | 184.9 | 847472 |
| 0.685 | 1.3165 | 28.297 | 184.8 | 847472 |
| 0.690 | 1.3179 | 28.296 | 184.7 | 847472 |
| 0.695 | 1.3194 | 28.295 | 184.6 | 847472 |
| 0.700 | 1.3208 | 28.296 | 184.7 | 990586 |
| 0.705 | 1.3223 | 28.297 | 184.9 | 990586 |
| 0.710 | 1.3237 | 28.299 | 185.2 | 990586 |
| 0.715 | 1.3251 | 28.302 | 185.4 | 990586 |
| 0.720 | 1.3265 | 28.305 | 185.6 | 990586 |
| 0.725 | 1.3279 | 28.309 | 185.8 | 990586 |
| 0.730 | 1.3293 | 28.314 | 186.0 | 990586 |
| 0.735 | 1.3307 | 28.319 | 186.2 | 990586 |
| 0.740 | 1.3321 | 28.325 | 186.4 | 990586 |
| 0.745 | 1.3335 | 28.332 | 186.6 | 990586 |
| 0.750 | 1.3348 | 28.339 | 186.8 | 990586 |
| 0.755 | 1.3362 | 28.347 | 187.0 | 990586 |
| 0.760 | 1.3375 | 28.355 | 187.2 | 990586 |
| 0.765 | 1.3388 | 28.365 | 187.4 | 990586 |
| 0.770 | 1.3402 | 28.374 | 187.6 | 990586 |
| 0.775 | 1.3415 | 28.384 | 187.8 | 990586 |
| 0.780 | 1.3428 | 28.395 | 188.0 | 990586 |
| 0.785 | 1.3441 | 28.406 | 188.2 | 990586 |
| 0.790 | 1.3454 | 28.418 | 188.4 | 990586 |
| 0.795 | 1.3467 | 28.430 | 188.6 | 990586 |
| z | ngz(z) | ngz(z,P1²) | ngz(z,P3²) |
|---|---|---|---|
| 3 | 1 | 0 | 1 |
| 5 | 2 | 1 | 1 |
| 7 | 2 | 0 | 2 |
| 9 | 2 | 1 | 1 |
| 11 | 3 | 1 | 2 |
| 13 | 3 | 1 | 2 |
| 15 | 3 | 1 | 2 |
| 17 | 4 | 2 | 2 |
| 19 | 2 | 0 | 2 |
| 21 | 4 | 2 | 2 |
| 23 | 4 | 2 | 2 |
| 25 | 4 | 1 | 3 |
| 27 | 5 | 2 | 3 |
| 29 | 4 | 3 | 1 |
| 31 | 3 | 0 | 3 |
| 33 | 6 | 3 | 3 |
| 35 | 5 | 2 | 3 |
| 37 | 5 | 2 | 3 |
| 39 | 7 | 3 | 4 |
| 41 | 5 | 2 | 3 |
| 43 | 5 | 1 | 4 |
| 45 | 9 | 3 | 6 |
| 47 | 5 | 2 | 3 |
| 49 | 3 | 1 | 2 |
| 51 | 8 | 4 | 4 |
| 53 | 6 | 3 | 3 |
| 55 | 6 | 2 | 4 |
| 57 | 10 | 5 | 5 |
| 59 | 6 | 3 | 3 |
| f | samples | pmax | c(f) | c(f)/c(1) | δ | dmax |
|---|---|---|---|---|---|---|
| 1 | 523586 | 7742923 | 0.6634 | 1.000 | 63.1 | 408.9 |
| 3 | 188583 | 2580973 | 1.3268 | 2.000 | 82.8 | 505.8 |
| 5 | 117563 | 1548577 | 0.8846 | 1.333 | 70.6 | 369.6 |
| 7 | 86163 | 1106129 | 0.7961 | 1.200 | 67.5 | 364.9 |
| 9 | 68365 | 860323 | 1.3268 | 2.000 | 82.7 | 451.5 |
| 11 | 56834 | 703897 | 0.7371 | 1.111 | 64.7 | 340.9 |
| 13 | 48776 | 595579 | 0.7237 | 1.091 | 65.0 | 350.7 |
| 15 | 42753 | 516193 | 1.7691 | 2.667 | 90.8 | 492.5 |
| 17 | 38121 | 455461 | 0.7077 | 1.067 | 63.8 | 331.6 |
| 19 | 34413 | 407521 | 0.7024 | 1.059 | 64.1 | 361.5 |
| 21 | 31435 | 368689 | 1.5922 | 2.400 | 87.6 | 479.2 |
| 23 | 28926 | 336649 | 0.6950 | 1.048 | 63.7 | 336.0 |
| 25 | 26782 | 309713 | 0.8845 | 1.333 | 70.8 | 349.2 |
| 27 | 24979 | 286771 | 1.3268 | 2.000 | 82.7 | 419.1 |
| 29 | 23394 | 266993 | 0.6880 | 1.037 | 62.8 | 329.7 |
| 31 | 22025 | 249763 | 0.6863 | 1.034 | 62.9 | 352.7 |
| 33 | 20800 | 234629 | 1.4743 | 2.222 | 85.2 | 498.1 |
| 35 | 19714 | 221219 | 1.0615 | 1.600 | 75.2 | 395.7 |
| 37 | 18741 | 209267 | 0.6824 | 1.029 | 62.8 | 312.7 |
| 39 | 17867 | 198533 | 1.4474 | 2.182 | 85.1 | 411.3 |
| 41 | 17068 | 188843 | 0.6805 | 1.026 | 62.6 | 299.8 |
| 43 | 16347 | 180053 | 0.6796 | 1.024 | 63.7 | 347.9 |
| 45 | 15671 | 172049 | 1.7691 | 2.667 | 90.5 | 489.1 |
| 47 | 15078 | 164743 | 0.6782 | 1.022 | 63.1 | 305.0 |
| 49 | 14524 | 158017 | 0.7961 | 1.200 | 67.1 | 377.5 |
| p = | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| q | z = ½(p+q) | |||
| 1 | 1 | 4 | 2 | 0 |
| 2 | 4 | 2 | 0 | 3 |
| 3 | 2 | 0 | 3 | 1 |
| 4 | 0 | 3 | 1 | 4 |
| p = | 1 | 2 | 4 | 5 | 7 | 8 |
|---|---|---|---|---|---|---|
| q | z = ½(p+q) | |||||
| 1 | 1 | 6 | 7 | 3 | 4 | 0 |
| 2 | 6 | 2 | 3 | 8 | 0 | 5 |
| 4 | 7 | 3 | 4 | 0 | 1 | 6 |
| 5 | 3 | 8 | 0 | 5 | 6 | 2 |
| 7 | 4 | 0 | 1 | 6 | 7 | 3 |
| 8 | 0 | 5 | 6 | 2 | 3 | 8 |
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 |
| 1 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 |
| 2 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 |
| 3 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 |
| 4 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 |
| 5 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 |
| 6 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 |
| 7 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 |
| 8 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 |
| 9 | 12 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 |
| 10 | 5 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 |
| 11 | 13 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 |
| 12 | 6 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 |
| 13 | 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 |
| 14 | 7 | 0 | 8 | 1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 |